Vie Boga - Milano '68 - Gogna

Sul "diedro bianco" della via Milano '68

Sulla "fessura gagliarda" della via Gogna

Medale
Parete S

La parete è una di quelle ormai diventate "storiche", e frequentata nelle cosiddette "mezze stagioni". Per sabato 25 era in programma la salita dalla via Boga, una delle poche non interessate dal progetto di sistemazione e riattrezzatura che ha ormai mutato faccia a queste pareti.

Dopo pochi tiri, disturbati da parecchia vegetazione e da una roccia di precaria qualità, capiamo che stiamo procedendo troppo lentamente. Segue consultazione e - con un po' di disappunto da parte mia, che mal sopporto di dover rinunciare ad un progetto - la decisione di spostarci sulla vicina "Milano '68". La musica cambia: via più impegnativa, ma su roccia affidabile e con migliori protezioni. Dopo due tiri attraversiamo la cengia di collegamento e passiamo sulla "Gogna", una via che avevo sempre guardato con timore, e tramite la quale raggiungeremo la cima del Medale.

A posteriori, la scelta è stata oculata, e la soluzione più che soddisfacente. Merito dei compagni di cordata, meno testardi del sottoscritto!

Relazione a breve sull'immancabile SB; qualche foto in più (grazie Matteo) sulla pagina G+.

Nota: quanto sopra è la relazione del percorso da me seguito. Altre opzioni possono essere possibili per quanto riguarda l'accesso, la salita e la discesa; inoltre, le protezioni, le soste ed il loro stato possono cambiare nel tempo: usate sempre le vostre capacità di valutazione! Vogliate segnalarmi eventuali errori ed omissioni. Grazie.

Trattoria del teatro

Piazza Mascheroni 3/A
Bergamo

Da qualche annetto non facevo visita alla "Trattoria del teatro" di Bergamo alta e mi sembrava di ricordare vagamente che l'ultima volta non mi aveva convinto del tutto. Anche qualche commento di amici mi faceva pensare ad un andamento un po' alterno. Ad ogni modo, sabato si è ripresentata l'occasione di verificare di persona, dopo aver assistito all'incontro con Albertazzi e Strinati al Teatro Sociale, e non me la sono fatta sfuggire. Risultato: decisamente positivo!

Non cercate il ristorante "stellato", il servizio raffinato, i piatti esotici, le ricche selezioni di vini blasonati: per quelli ci sono altri (ottimi) posti dove andare. Se però volete assaggiare la cucina locale, del territorio (si potrebbe dire "tipica" se il termine non fosse diventato odioso e insignificante), allora non mancate di visitare questo posto come faceva sempre il Maestro Gavazzeni, ricordato in un articolo recente del Corriere. Interni rustici, clientela in massima parte locale, un pizzico di burberia della signora che prenderà le ordinazioni, lista ristretta sia per i piatti che per i vini (predilezione per quelli del nord Italia). Ma - per quel che mi riguarda - i tagliolini ed il capretto erano ottimi, come hanno convenuto anche i nostri commensali di Roma! Peccato che il dessert si riduca ad un paio di scelte (gelato o crème caramel), per quanto ben fatte.
Infine, poiché la modernità si insinua anche nei posti più inusitati... udite udite... ultimamente al Teatro accettano anche il pagamento con Bancomat o carte di credito! Ma non fateci troppo affidamento: il sistema è un po' malfunzionante.

Marshall 5010 - Controllo toni

Fig.1: Schema del circuito di controllo-toni

Continuo qui la chiacchierata sullo schema del 5010 iniziata con il preamplificatore dando un'occhiata alla parte di controllo-toni. Lo schema, piuttosto semplice, è indicato nella Fig.1 ed è un buon esempio di come si possano ottenere discrete prestazioni anche con pochissimi elementi, se il circuito è ben progettato. I valori dei componenti sono:

• C₉ = 4.7 nF, C₁₀ = 220 pF, C₁₁ = C₁₂ = 47 nF
• R₁₁ = 68 kΩ, R₁₄ = 4.7 kΩ
• VR₃ = 220 kΩ
• VR₄ = 22 kΩ
• VR₅ = 1 MΩ (log)

Anche se lo schema è molto semplice, una soluzione analitica restituisce espressioni piuttosto complicate; cerchiamo quindi di capire come funziona la rete in modo approssimato, per poi verificare i risultati con i calcoli corretti.

Alti
Il regolatore degli alti è costituito dal ramo C₁₀-VR₃, che filtra passa-alto il segnale di ingresso. Per determinare l’uscita, però, dobbiamo prima valutare la tensione a valle del potenziometro VR₃, che chiameremo V₅. Per questo, consideriamo il circuito semplificato per alte frequenze, ottenuto cortocircuitando i condensatori di valore più elevato (C₁₁ e C₁₂) ed eliminando il ramo C₁₀-VR₃, ad alta impedenza: esso risulta costituito da C₉ in parallelo a x₄ VR₄ (trascuriamo VR₅ perché di valore elevato e indichiamo con la variabile x l'effetto del potenziometro). Da qui è facile vedere che il trasferimento su V₅ è piccolo: nel caso di x₄ = 1 si ha V₅ ≈ V_i/4, ma il trasferimento crolla dopo la frequenza corrispondente al polo di C₉, ovvero

Se diminuiamo x₄, d’altra parte, la frequenza del polo aumenta, ma il trasferimento in continua diminuisce ed il risultato non cambia. Ciò significa che, in prima approssimazione, V₅ si può considerare come cortocircuitato a massa. Il circuito semplificato per il calcolo del trasferimento degli alti diventa quindi quello indicato in Fig.2, con il filtro C₁₀-VR₃ connesso tra ingresso e massa, sicché il risultato finale è

Fig.2: schema semplificato per il calcolo degli alti

Fig.3: Trasferimento approssimato per gli alti

indicato in Fig.3 per x₃ = 0.1, 0.5, 1. Il polo del trasferimento è fissato a

indipendentemente dal valore di x₃ e, in prima approssimazione, da quello degli altri componenti; la regolazione incide solo sul guadagno ad alte frequenze. Per frequenze inferiori ad f₉, poi, l’approssimazione può cadere in difetto; siamo nell'intervallo di frequenze controllato dai medi.

Medi
Il regolatore delle medie frequenze è il potenziometro VR₄. Per capire come lavora sul segnale, spostiamoci a frequenze minori di f₉: ora i condensatori C₉ e C₁₀ si comportano come circuiti aperti, e l’uscita è uguale alla tensione V₅. Inoltre, la resistenza x₅ VR₅ è molto maggiore di x₄ VR₄ (tranne che per i casi-limite in cui x₅ < 0.022 x₄, cioè quando x₅ è praticamente nullo) e possiamo considerarla come un circuito aperto; su C₁₁ non c’è caduta (o, se preferite, il polo relativo è a bassa frequenza) e la rete diventa la semplice serie di R₁₁, C₁₂ e x₄ VR₄, come indicato in Fig.4.

Fig.4: Schema semplificato per il calcolo dei medi.

Fig.5: Trasferimento approssimato dei medi

La tensione di uscita è data da:

cioè una rete polo-zero il cui guadagno a frequenze maggiori delle singolarità introdotte da C₁₂ è dato dalla partizione resistiva tra x₄ VR₄ e R₁₁. Il trasferimento sopra indicato è riportato in Fig.5 per x₄ = 0.1; 0.5; 1. Stavolta la regolazione cambia sì il guadagno alle medie frequenze, ma modifica anche il limite inferiore della banda. Val la pena notare come, a differenza di quanto avviene per le altre bande di frequenza, i medi sono sempre attenuati, e anche per x₄ = 1 la risposta in frequenza non raggiunge mai gli zero dB. Inoltre, la regolazione non ha effetto sulle basse frequenze (la posizione del polo non dipende fortemente da x₄.

Bassi
Sono regolati dal potenziometro VR₅. Il comportamento alle basse frequenze può essere trattato analogamente a quanto fatto per le medie: iniziamo quindi ad eliminare i condensatori C₉ e C₁₀, che si comportano come circuiti aperti, e consideriamo il ramo R₁₁, C₁₁, VR₅ (trascuriamo anche R₁₄, che entra in gioco solo per valori molto piccoli di x₅, e consideriamo per il momento C₁₂ come circuito aperto): la rete è analoga alla precedente, ma stavolta l’uscita è prelevata a valle del condensatore, comportandosi da filtro passa-alto (si veda lo schema in Fig.6). Il trasferimento diventa quindi:

Fig. 6: Schema semplificato per il calcolo dei bassi

Fig.7: Trasferimento approssimato dei bassi

riportato in Fig.7 per x₅ = 0.1; 0.5; 1. Anche in questo caso il potenziometro VR₅ modifica la costante di tempo, e non solo il guadagno del filtro, che ha comunque una variazione molto più ridotta rispetto ai casi precedenti. Si può poi notare che l’effetto di VR₅ sul trasferimento è assai non-lineare: piccolo finché VR₅ ≫ R₁₁ e più sensibile poi; credo che sia per questo motivo che il potenziometro VR₅ è di tipo logaritmico, ovvero con una variazione della resistenza non lineare con la posizione del cursore; si introduce così una prima compensazione della non-linearità, “raddrizzando” in parte la dipendenza da x₅. É infine doveroso ricordare che questa trattazione, così come la precedente, trascura le interazioni tra i due condensatori: le posizioni reali dei poli e degli zeri sono quindi lievemente differenti rispetto a quanto calcolato.

Fig.8: Trasferimento corretto per x₃ = 0.1; 0.5; 1 e x₄ = x₅ = 0.5
(tonalità di azzurro) con relative approssimazioni. Le curve per
gli alti sono le stesse della Fig.3.

Fig.9: Trasferimento corretto per x₄ = 0.1; 0.5; 1 e x₃ = x₅ = 0.5
(tonalità di azzurro) con relative approssimazioni. Le curve per
gli alti sono le stesse della Fig.5.

Fig.10: Trasferimento corretto per x₅ = 0.1; 0.5: 1 e x₃ = x₄ = 0.5
(tonalità di azzurro) con relative approssimazioni. Le curve per
gli alti sono le stesse della Fig.7

Andamento complessivo
Il motivo dei calcoli riportati fin qui, con tutte le loro approssimazioni, era di dare (o tentare di dare) un’idea abbastanza corretta del perché il circuito funziona. Per finire questa parte, confrontiamo i risultati che si ottengono “componendo” i trasferimenti nelle varie regioni di funzionamento con quanto risulta dalla soluzione completa della rete. La Fig.8 mostra il risultato della soluzione analitica della rete in esame per x₄ = x₅ = 0.5 e x₃ che assume i tre valori fin qui considerati: 0.1; 0.5; 1 (rispettivamente, le curve celeste-azzurro-blu). Sono anche riportate le approssimazioni fin qui calcolate: si vede che il comportamento complessivo segue abbastanza fedelmente l’inviluppo delle caratteristiche nelle tre regioni. La stessa conclusione si può trarre dalle Figg.9 e 10, dove il confronto è condotto modificando, rispettivamente, x₄ e x₅, tenendo gli altri parametri al valore 0.5. Si noti la differenza nella posizione dello zero dei medi (così come dei poli, anche se meno evidenti) dovuta all'interazione tra C₁₁ e C₁₂, e come il circuito tenda ad attenuare le medie frequenze rispetto alle basse ed alle alte: questo mi pare essere il motivo che spiega l’andamento opposto osservato nello stadio di preamplificazione.

Prossimamente andremo a considerare lo stadio di "presence".

Basilicata IGT Canneto 2001 D'Angelo

In vino veritas

Nonostante i miei vini preferiti si trovino al "nord" (come eguagliare un barolo o un pinot nero?), essi sono seguiti ad un'incollatura dalle varie manifestazioni dell'aglianico, sia sul versante irpino che lucano. Con piacere, quindi, in occasione di un'ormai piacevole consuetudine che mi vuole spesso invitato a pranzo ad approfittare delle capacità culinarie di Amedeo, decido di... verificare le condizioni di invecchiamento di questa bottiglia. Nonostante la denominazione sia "Basilicata IGT", il vitigno è aglianico al 100%... e si sente! Tuttavia, rispetto ad altri vini dello stesso "lignaggio", il Canneto si presenta ruvido, quasi scostante al primo approccio, chiuso nel suo territorio di vecchie viti che richiede un lento avvicinamento. Ma alla fine si viene ripagati; non aspettatevi però un "peso massimo" di concentrazione e di persistenza (eccheppalle 'sti vini tutti uguali, no?), ma onesti aromi di spezie e qualche frutto. Purtroppo, causa il gelo che imperversa da queste parti ed il mio protervo avvicinamento a piedi alla magione del mio anfitrione, ho assaggiato il vino un po' troppo freddo, ed i sapori ne hanno risentito, per risvegliarsi verso la fine della bottiglia, quando le già scarsissime capacità di analisi enologica del sottoscritto erano annegate da tempo. Peccato. Ma c'è sempre una seconda occasione...

Uomini e folle di guerra

di Angelo Gatti
Mondadori, Milano, 1932

Era un po' di tempo che non tornavo ad una lettura sulla prima guerra mondiale, e questo libro riposava ormai da troppi mesi sullo scaffale. Angelo Gatti fu a capo dell'ufficio storico del Comando supremo durante la Grande Guerra, e scrisse una serie di libri e diari (che dovrò leggere) molto interessanti, grazie al punto di vista privilegiato dell'autore. Questo libro è forse il suo più famoso, molto citato nella storiografia della Grande Guerra; pure, i capitoli veramente interessanti sono pochini: quello su Caporetto, che costituisce forse la prima lucida analisi delle responsabilità di Badoglio nel disastro, e quello sulla Strafexpedition, anche se un po' troppo rassicurante e "ufficiale". Soporiferi invece i cosiddetti "ritratti psicologici" che ossessionavano anche il Gatti (mediocre) romanziere: su Napoleone, Ludendorff, Vittorio Emanuele II e Diaz le pagine volano via tra iperboli e descrizioni caratteriali che nulla aggiungono alla conoscenza del personaggio (ammesso che uno ne sia interessato; per quel che mi riguarda l'unica cosa rilevante dell'era napoleonica è l'arte dello Stile Impero...). In mezzo stanno gli altri capitoli: un paio su Garibaldi e Cavour (più o meno tornati di moda) e un paio (migliori) sulle relazioni di Francesco Giuseppe e Falkenhayn cogli italiani prima della loro entrata in guerra, fonti di ulteriore scoramento per le utili informazioni che non furono da noi usate per evitare in parte i macelli dei primi mesi di guerra. La prosa e la lettura scorrono comunque fluidamente; bisogna dare atto al Gatti di avere proprietà di linguaggio e di scrittura, doti non comuni tra i generali italiani del tempo.

Marshall 5010 - Preamplificatore

L'aver dovuto riportare in vita il vecchio amplificatore per chitarra mi ha fornito l'occasione per dare un'occhiata, seppur al prim'ordine, allo schema. Un po' per curiosità, un po' per interesse, ne ho poi approfondito il funzionamento, e lo descrivo nel seguito; l'idea è di mantenere la spiegazione ad un livello comprensibile a chi (studenti e non) abbia una minima familiarità con i circuiti elettronici e le funzioni di trasferimento, facendo vedere come funziona un oggetto semplice, ma "reale". Questo primo post è dedicato allo stadio di ingesso e preamplificazione; inserirò poi qualcosa sullo stadio di controllo toni, di presence e - con calma - su quello finale di potenza.

Fig.1: schema del preamplificatore

La versione di amplificatore Marshall 5010 in mio possesso è anteriore e presenta solo lievissime differenze (tutte concentrate nel preamplificatore) rispetto allo schema che si trova su internet, ma tutti i nomi (o etichette) dei componenti sono diversi, sì da sconsigliare ogni operazione sull'amplificatore che sia basata su tale schema. Lo schema "corretto" del preamp. è indicato in Fig.1. Esso è costituito da due stadi realizzati con amplificatori operazionali (AO) in configurazione non-invertente. Si può notare il potenziometro VR₁ inserito nell’anello di reazione di AO1, che regola il guadagno del primo stadio; il secondo stadio è invece a guadagno fisso. I valori dei componenti sono:

• C₁ = 47 nF, C₂ = C₃ = 2.2 μF, C₄ = 2.2 nF, C₅ = 100 pF, C₆ = 2.2 μF
• R₁ = 1 MΩ, R₂ = R₃ = 68 kΩ, R₄ = 10 kΩ, R₅ = 100 Ω, R₆ = 22 kΩ, R₇ = 10 kΩ, R₈ = 470 Ω
• VR₁ = 22 kΩ
• AO = CA1458E (obsoleto e sostituibile con MC1458)

Ingresso

Iniziamo ad osservare la rete di ingresso con i due deviatori corrispondenti agli ingressi HIGH (su R₃) e LOW (su R₂). Quando si utilizza l’ingresso HIGH il generatore vede una partizione tra 34 kΩ parallelo delle due resistenze di 68 kΩ) e 1 MΩ, e si ritrova praticamente inalterato all'ingresso non-invertente di AO1; se si utilizza l’ingresso LOW si ha invece un’attenuazione di un fattore 2. Naturalmente questa differenza esiste solo se si utilizza un ingresso per volta; se si suona in due gli interruttori sono aperti ed entrambi gli ingressi sono attenuati (pensate alla sovrapposizione degli effetti, per quanto poi dovremmo discutere dell'impedenza della sorgente). Un altro commento che si può fare su questo semplice stadio è la possibilità di usare l’ingresso LOW come uscita per porre in cascata più amplificatori.

1° stadio

Veniamo ora ad AO1. Se indichiamo con x₁ la frazione di VR₁ connessa tra il morsetto centrale (a massa) e il terminale alla sua destra nello schematico, ovvero l’ingresso di AO2, e chiamiamo per semplicità Z₁ la quantità R₅ + (1 - x₁) VR₁ si ottiene immediatamente il guadagno ideale del primo stadio di amplificazione:

Fig.2: Trasferimento del 1° stadio di preamplificazione

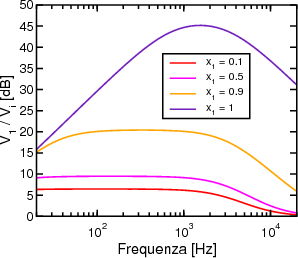
Fig.3: Guadagno del 1° stadio

La funzione di trasferimento è riportata in Fig.2 e ha due poli e due zeri, le cui posizioni sono:
p₁ = 1/(2πC₃Z₁);            p₂ = 1/(2πC₄R₆)
z₁ ≈ 1/(2πC₃(Z₁ + R₆));  z₂ ≈ 1/(2πC₄(Z₁//R₆))
Il primo zero è sempre a frequenze dell’ordine di 1-2 Hz e non compare sul grafico; si noti però che il trasferimento in continua è unitario e non nullo; questo serve ad evitare problemi di saturazione dello stadio legati ad offset e bias dell’operazionale. Il limite superiore alla banda-passante, p₂, è indipendente da x₁ ed è posizionato a circa 3.3 kHz, mentre il guadagno a centro-banda

G₁ = 1 + R₆/Z₁ = 1 + R₆/(R₅ + (1 - x₁)VR₁)

varia da 2 a 220 al variare di x₁ (Fig.3; forse un potenziometro logaritmico avrebbe potuto attenuare in parte la non-linearità, ma tenete presente che gli alti guadagni servono per distorcere il segnale). Si noti che il prodotto guadagno-banda degli operazionali utilizzati è di circa 1 MHz, che darebbe una banda passante di circa 5 kHz nel caso G₁ = 200; la soluzione adottata garantisce una banda indipendente dall'amplificazione, demandando l’elaborazione del segnale alla sezione di controllo-toni (nel caso di x₁ = 1 il trasferimento reale è lievemente modificato per via del ridotto guadagno d’anello, ma evitiamo di riportare qui i calcoli). Ciò detto, la banda passante sembrerebbe effettivamente pochina: anche se la frequenza principale di una chitarra elettrica non supera gli 1.1 kHz, si devono considerare le armoniche, particolarmente importanti quando interviene la distorsione. Forse un aumento, anche solo di un fattore 2, sarebbe interessante da “sentire”, ma immagino che Jim Marshall ne sapesse assai più di me su queste cose.
Altro aspetto da notare è la deformazione della risposta in frequenza ad altissimi guadagni: per G₁ = 220 il primo polo si sposta ad una frequenza di circa 720 Hz, avvicinandosi al secondo e determinando la forma che si vede in figura. È però vero che questo si verifica solo con il Preamp volume a totale saturazione: già per x₁ = 0.95, ad esempio, G₁ scende a 20, p₁ si posiziona a 60 Hz (il mi basso è a circa 82 Hz) e la distorsione è già più che sensibile. Se utilizzate il primo stadio in saturazione, quindi, usate adeguatamente il controllo-toni per compensare la risposta in frequenza (ma ve ne accorgerete anche “ad orecchio” che c’è una compressione dei toni alti e bassi).

Equalizzazione
Tra i due amplificatori operazionali è posta una rete (che chiamiamo di "equalizzazione" in mancanza di un nome migliore) composta dai condensatori C₁ e C₂ e dalle resistenze R₄ e x₁VR₁. Anche in questo caso il trasferimento è elementare, ma iniziamo a valutare il polo associato a C₂: la resistenza ai suoi capi è, nel caso minimo, 10 kΩ, che porrebbe il polo a circa 7 Hz. Possiamo quindi trascurarlo ed ottenere il trasferimento come

Fig.4: Trasferimento dell'ingresso del 2° stadio

ovvero un partitore che azzera il volume di uscita per x₁ = 0 (dove G₁ è unitario) ed una coppia zero-polo. Il trasferimento totale fino all'ingresso del 2° stadio di preamplificazione è riportato in Fig.4 (le linee tratteggiate sono le stesse della Fig.3).

2° stadio
Il secondo stadio di preamplificazione è identico al primo, con solo un diverso valore dei componenti; la funzione di trasferimento è quindi

Fig.5: Trasferimento complessivo del preamplificatore

Stavolta il guadagno a centro-banda è fisso e pari a circa 20, mentre il limite superiore alla banda passante dato da C₇ R₅ si trova a 160 kHz e non interviene (in pratica la banda è limitata dall’operazionale stesso a circa 50 kHz, e C₇ può essere stato inserito per migliorare la stabilità). Il polo che limita inferiormente la banda, però, si trova ora a circa 154 Hz, ed introduce un taglio sulle frequenze inferiori. Il trasferimento complessivo dello stadio di preamplificazione (1^∘ stadio, "equalizzazione", 2^∘ stadio) è indicato in Fig.5 per diversi guadagni. Il motivo per cui il trasferimento non è piatto in frequenza è forse da ricercare in una specie di compensazione del trasferimento della rete successiva di controllo-toni, che deprime le medie frequenze rispetto a quelle basse e alte, anche se non è da escludere che si tratti semplicemente di una scelta che dà un "suono migliore".
L’ultimo commento è relativo al guadagno: il secondo stadio ha un guadagno fisso pari a 20 per permettere di ottenere la distorsione ad alti guadagni G₁ e bassi volumi di uscita. Teniamo presente che l’alimentazione è di ±20 V, quindi si entra in distorsione quando l’uscita del primo stadio giunge circa a ±1 V; con il massimo guadagno di 220 ciò corrisponde a circa 4.5 mV in ingresso, valore tranquillamente raggiungibile dalle chitarre elettriche. Lo stadio che distorce, tecnicamente, è quindi il secondo. Per pignoleria si può anche verificare lo slew rate dell’operazionale, pari a circa 0.8 V/μs, che si trasforma in una banda di piena dinamica di circa 6.3 kHz, ben al di sopra del polo dell’amplificatore e della banda del segnale.

Nel prossimo post diamo un'occhiata allo schema di controllo toni.

Vallée d'Aoste DOC Donnas 2002 Caves cooperatives de Donnas

Un vino da blues

La domanda è la seguente: vi trovate con un vecchio amico a ripercorrere strumenti e repertori musicali che avevate più o meno abbandonato dopo gli anni di Università, avendo cura di evacuare per tempo donne e bambini, e passate un pomeriggio rispolverando precarie capacità di improvvisazione su armonie rock-blues - che per fortuna possono essere piuttosto semplici.

Che vino scegliete per accompagnare questa "esibizione"?

Io mi sono presentato da Sergio con un Donnas 2002, che non è sopravvissuto fino alla fine del pomeriggio. Non so se abbia migliorato o meno la qualità dei nostri assoli - anche se peggiorarla sarebbe stato arduo - ma certamente ne ha ridotto la durata garantendoci numerose pause di "degustazione".

Ma veniamo al vino: si beve con molta piacevolezza nonostante l'età e l'annata (il 2002) che non è stata certo una delle migliori. Dategli un poco di tempo dopo l'apertura (e dopo un blues in qualche chiave insolita) e ne apprezzerete il corpo ed il sentore vagamente speziato. È probabilmente il vino più noto e più facilmente reperibile tra quelli (e non sono pochi) della Val d'Aosta, che resta per me una regione fantastica, per il cibo, il vino, le arrampicate... 

Alpi Orobie

di Silvio Saglio, Alfredo Corti e Bruno Credaro
CAI-TCI, Milano, 1957

Quando sono finalmente riuscito a "mettere le mani" su una copia dell'ormai storica guida delle alpi Orobie, mai più ristampata dal lontano 1957, sapevo più o meno cosa aspettarmi. Una guida di quegli anni, peraltro uscita "già vecchia" perché basata su materiale di quasi un ventennio precedente, può avere solo un modestissimo valore dal punto di vista prettamente alpinistico; l'interesse è innanzitutto storico e poi, perché no, affettivo, visto che si parla delle montagne "di casa" tante volte salite per quasi tutti i sentieri e poi quasi dimenticate quando le mie (pur pessime) capacità alpinistiche hanno spostato altrove il baricentro delle mie frequentazioni.

Giunto alla fine del libro, devo però dire che vi ho trovato parecchi spunti che potrebbero forse essere interessanti: diverse le vie di salita che non si ritrovano nel successivo "88 immagini per arrampicare" e che, a sentirne la descrizione, invogliano quanto meno a darvi un'occhiata. Riporto di seguito questi itinerari, che sono classificati come "difficili" o "molto difficili". Nonostante una comparazione non sia immediata, e visti gli anni in cui la guida è stata scritta, si può pensare che nel primo caso si possano incontrare difficoltà di IV e nel secondo di V o più (purtroppo la guida non riporta la difficoltà se non per pochissimi itinerari); si tratta quindi di salite abbordabili, almeno in teoria... tenendo sempre presente che spesso la roccia delle orobie è poco affidabile (più o meno come questa guida).

- Pizzo tre signori - la sfinge: parete NO (Gallotti, Broggi, Barenghi, 1940). Anche parete SE (Tettamanti, 1956)

- Dente S di Trona: parete N (Giudici, ?). Da concatenare con gli altri per uno sviluppo decente...

- Pizzo di Trona: parete NE (Faverio, De Simoni, Beretta, 1930)

- falso Trona: parete N (?). Il versante E è dato come inviolato... che ne è 55 anni dopo?

- Torre del lago: parete E (come sopra)

- Pizzo di Tronella: cresta N + parete NE del Dente (forse Fasana e Mariani, 1910). Anche parete NO del Dente (Parravicini, Tagliabue, Ruscelli, Bianchi, De Simoni, 1930) e cresta S (Scalvini, 1913)

- Dente di mezzaluna: parete N (Paltrinieri, Del Nero, 1955). Questo itinerario è riportato anche in "88 immagini per arrampicare" con difficoltà di III+, ma con percorso diverso.

- Torrione di Mezzaluna: parete N (Faverio, Parravicini, De Simoni, Tagliabue, 1931) e pareti N+E+S (Guenzati, 1923)

- Pizzo di mezzaluna: parete O (Gallotti, Cattaneo, 1941)

- Denti della vecchia: traversata da N a S (Citterio, Tagliabue, De Simoni, 1931) e diedro NO del dente S (stessi salitori della traversata). Anche qui difficoltà contrastanti rispetto a "88 immagini..."

- Cima di Pescegallo: parete ONO, sia per il diedro che per fessura (entrambi Fasana, Omio, 1931)

- Monte Ponteranica occidentale: cresta S (Fasana, Sala, 1930)

- Dentino di Ponteranica: parete N (Fasana, 1931)

- Monte Cabianca: due vie sulla parete N (N. e G. Cattaneo, 1948 e Longo, De Molfetta, 1950)

- Pizzo Poris: cresta E (Longo, Martina, 1952), parete N (Longo, Demolfetta, 1951),

- Corno Stella: parete NE (Galli-Valerio, Rossi, 1910). Via senza ripetizioni (almeno fino al '57)... cosa pensare?

- Pizzo di Cigola: parete NE, anch'essa inviolata al '57...

- Piz Cavrin: parete N (Gualzetti, Melazzini, 1933)
- Dente di Coca: parete N (Longo, Cornago, 1932). La corda metallica del canale della cresta E esisterà ancora?
- Cime di q. 2685 e 2658 m a SO del pizzo tre confini: sono date come inesplorate...